第一原理計算手法の新規開発
第一原理多成分系分子軌道法
分子軌道の概念を、プロトンや陽電子といった多成分系に拡張することで、核の量子揺らぎや陽電子の量子効果も柔軟に表現することを可能としました。
第一原理分子軌道(ab initio molecular orbital, MO)法は、分子内の多数の原子核と電子の間の相互作用をなるべく少ない近似を用いて解く手法です。近年の分子軌道理論の発展による高精度化、および高速・大容量計算機の急速な発達に伴い、分子軌道法は電子状態や分子構造さらには化学反応素過程を含む様々な状態を理論的に予測・解明できるようになりました。そしてその精度は、実験と比較して、いわゆる化学的精度といわれるkcal/molの誤差範囲で比較できるレベルとなっています。
私たちの開発している第一原理多成分系分子軌道(ab initio multi-component molecular orbital, MC_MO)法は、従来電子に適用していた分子軌道(一電子軌道)の概念を、プロトンやミューオン、陽電子といった質量の軽い粒子にも拡張し、それら粒子を含めた多成分系を量子力学的に解析することを可能としました。従来の分子軌道法では、電子のみを量子力学的に取り扱いますが、核は点電荷としてしか扱えません。一方、多成分系分子軌道法を用いることで、電子だけでなく、核自身の量子揺らぎや陽電子自身の量子効果も柔軟に表現することができます。
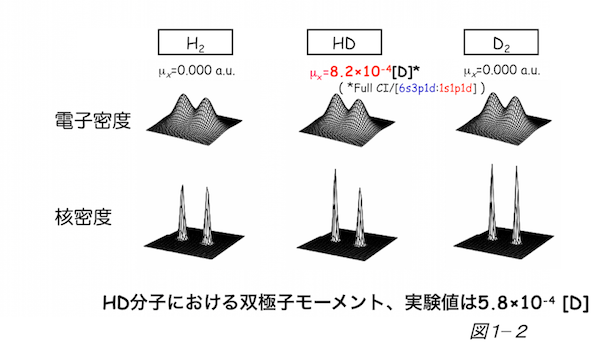
本手法は平均場近似を用いた一粒子近似に基づいた表式をしているので、多体効果を取り込むには、従来の分子軌道法で構築された電子相関理論を適用することができます。多成分系分子軌道法で多体効果を取り込むためには、電子相関だけでなく、電子-プロトン相関(電子-陽電子相関)といった興味深い異種粒子間の多体効果を考慮しなければならなりません。私たちは既に摂動法や、変分法に基づく配置間相互作用法を駆使することにより、振動・電子励起状態を同時に求め、さまざまな水素系の同位体効果の解析を行ってきた。その一例として、本手法では、H/D同位体効果を柔軟に表現することを可能としました。H2分子やD2分子の構造の違い、さらにはHD分子の双極子モーメントの実験値を良く再現することができました。(図1-2)また陽電子化合物に適用することにより、有機分子や生体分子への陽電子親和力を理論的に求めることに成功しました。
第一原理経路積分法
核の量子揺らぎに経路積分法を、電子に分子軌道を適用することで、有限温度のもとで核・電子全自由度を量子力学的に取り扱うことを可能としました。
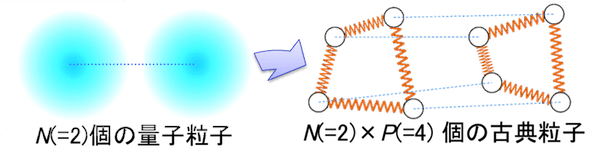
経路積分分子動力学法は、断熱近似のもとでFeynmanによって提案された量子力学の枠組みである経路積分法を利用して、核の量子効果を取り込む手法です。この手法では、波動的なふるまいをする1個の量子的原子核の統計的性質は、互いにバネで繋がったP個の古典的原子核(ビーズ)の統計的性質で表すことができる、という等価原理を基礎としています。
私たちが研究している第一原理経路積分分子動力学 (ab initio path integral molecular dynamics, ab initio PIMD)法は、経験的ポテンシャル関数を一切用いずに、非経験的に電子状態を解きつつ、断熱近似のもとで経路積分分子動力学法を実行する手法です。本手法では統計平均を取ることにより、電子・核全自由度の量子力学的取り扱いを可能とするだけでなく、温度揺らぎも考慮することができるといった利点があります。
経路積分計算においては、一般的に分配関数の2次展開が用いますが、低温においてはビーズ数の収束性が遅いことが知られています。そこで私たちは、4次展開により収束性を速め、またハイブリッドモンテカルロ法を適用することで、精度を保ったまま計算時間を抑えることに成功しました。
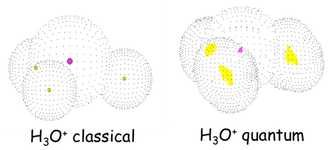
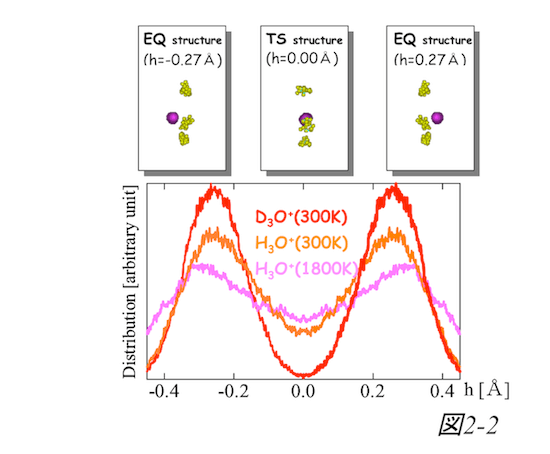
第一原理的に電子状態を求めることで、反応経路近傍のポテンシャル曲面を高精度で系統的に改善していくことが可能となります。本手法を用いて、様々な低障壁水素結合系の解析を行いました。例えばH3O+のWalden反転の様子を示します(図2-2)。重水素置換体だと殆ど反転しないのに対し、軽水素体、さらには高温にすると反転が頻繁にサンプルされる様子が解ります。
第一原理多成分量子モンテカルロ法
量子モンテカルロ法を多成分系に拡張することにより、多成分系化合物の数値的な変分エネルギーの厳密解を算出することを可能としました。
量子モンテカルロ(Quanum Monte Carlo; QMC)法は、現在最も精密な解を得られる第一原理計算手法の一つであり、孤立系(原子、分子)・周期系(固体)をとわず適用可能な、汎用性の高い、高精度理論手法です。従来の分子軌道法では十分に取り込む事が困難であった電子-陽電子相関といった多成分間の多体効果も、QMC法により高精度に取り込むことが可能となります。ここでは、私たちが開発した多成分系量子モンテカルロ法の例を踏まえ、一般的に良く利用されている変分モンテカルロ(Variational Monte Carlo; VMC)法と拡散モンテカルロ(Diffusion Monte Carlo; DMC)法について簡単に紹介します。
VMC法は、変分パラメータを含む試行波動関数による物理量の期待値をモンテカルロ積分によって評価する手法で、その原理・アルゴリズムは単純です。試行波動関数として一般的に良く用いられるのはSlater-Jastrow型関数で、これは分子軌道計算などであらかじめ得た単一(または複数)のSlater行列式に、多体効果を取り込むためのJastrow相関因子を付与した関数形です。Jastrow相関因子に含まれる変分パラメータ等を最適化することで、そのパラメータ空間内での変分的な波動関数を得ます。VMC法では、原子系に対してはおおむね60~80%程度の相関エネルギーを取り込めます。
DMC法では、時間依存シュレーディンガー方程式の虚時間発展を利用することで、VMC法で得られた試行波動関数をより正確な固有状態へと射影します。DMC法では、波動関数の虚時間発展を古典粒子の拡散・分岐過程とみなします。原理上は厳密な基底(あるいは励起)状態のエネルギー固有値を算出することが可能です。実際には配置数変動や電子のフェルミオン性に起因した節固定近似などによる誤差が伴うものの、おおむね95%以上の相関エネルギーを取り込めます。
私たち開発した多成分系量子モンテカルロ法は、多電子系に対するQMC法を多成分系化合物へと拡張させたものです。例えばHCN分子に陽電子を付着させた計算を実行したところ、従来の変分エネルギーよりも、0.5 Hartreeも低い、数値的に厳密なエネルギーを求めることに成功しました。(図3-2)

プロジェクト
省庁等からの研究費
-
科学技術振興機構(JST)、戦略的創造研究推進事業CRESTタイプ、2023~2028年度
「Giant CISS物質: 界面陽電子・電子の全運動量制御」
主たる共同研究者:立川 仁典 (研究代表者:関 修平) -
文部科学省、スーパーコンピュータ「富岳」成果創出加速プログラム、2023~2025年度
「燃料電池触媒層の物質輸送機構解明に向けた、マルチスケール計算技術構築とその活用」
研究分担者:島崎 智実 (研究代表者:藤本 和士) -
科学技術振興機構(JST)、戦略的創造研究推進事業CRESTタイプ、2022~2027年度
「デバイスインバースデザインのための表界面稼働状態計測解析法の確立」
主たる共同研究者:立川 仁典 (研究代表者:多田 朋史) -
産業技術総合開発機構(NEDO)、大学発事業創出実用化研究開発事業費助成金、2021~2024年度
「鉛フリー・アロイ化錫ペロブスカイト・タンデム太陽電池の国際共同研究開発」
研究分担者:島崎 智実 (研究代表者:早瀬 修二)
科学研究費助成事業(学術研究助成基金助成金)
-
課題番号:23H03993 学術変革研究A(公募研究) 2023~2024年度
「水素の量子効果を考慮した新規量子化学による星間分子雲における重水素濃縮機構の解明」
研究代表者:立川仁典 -
課題番号:23K17905 挑戦的研究(萌芽) 2023~2024年度
「量子多成分系分子理論とデータ科学の融合による低障壁水素結合系の物性発現機構の理解」
研究代表者:立川仁典 -
課題番号:23H05462 基盤研究(S) 2023~2027年度
「スピン偏極陽電子ビームを基軸とする新しいサイエンスの展開」
研究分担者:立川 仁典 (研究代表者:河裾 厚男) -
課題番号:23K13827 若手研究 2023~2025年度
「水素吸蔵材料開発に向けた経路積分法と機械学習の融合プログラムの開発」
研究代表者:桑畑 和明 3600 -
課題番号:22K05038 基盤研究(C) 2022~2024年度
「第一原理計算およびデバイス・モデルによる非フラーレン・アクセプター材料の機能解明」
研究代表者:島崎 智実 -
課題番号:21K04983 基盤研究(C) 2021~2023年度
「量子モンテカルロ法の高度化による多原子分子に対する計算陽電子分光法の確立と展開」
研究代表者:北幸海 -
課題番号:21H00026 新学術領域研究(研究領域提案型) 2021~2022年度
「高精度予測に向けた量子多成分系分子理論の高度化による高次水素機能の発現機構解明」
研究代表者:立川 仁典 -
課題番号:22KJ2564 特別研究員奨励費 2021~2023年度
「星間分子雲における重水素体濃縮機構解明のための新しい量子化学計算手法の開発」
研究代表者:桑畑 和明
論文
こちらをご覧ください.
Proceeding
こちらをご覧ください.
解説・総説
こちらをご覧ください.
学会発表
こちらをご覧ください.